獨立事件的排列組合分析
[排列組合]問題中,常須考慮「進」與「出」的排列方式。因進出為獨立事件,最後結果可乘算求得。
進門:
* 甲先進門:5種選擇,乙進門則扣除甲選擇的門,剩4種。總計:20 (5 x 4)
* 甲乙不得同門:
* 甲出乙進的門:甲1種選擇,乙4種。總計:4 (1 x 4)
* 甲不走乙進的門,也不走甲進的門:甲3種選擇,乙3種。總計:9 (3 x 3)
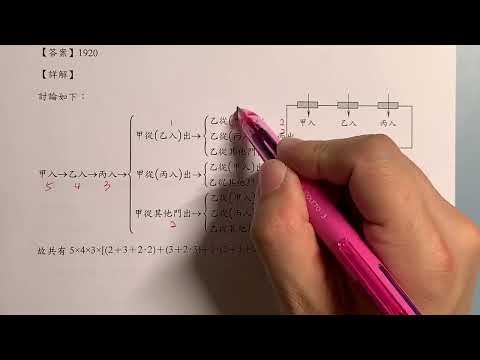

出門:
* 甲出乙進的門:1種選擇,乙4種。
* 甲不走乙進的門,也不走甲進的門:甲3種選擇,乙3種。
總結:
| 情況 | 甲進門 | 乙進門 | 甲出門 | 乙出門 | 總計 |
|—|—|—|—|—|—|
| 甲先進門 | 5 | 4 | 1 | 4 | 20 |
| 甲乙不得同門 | 1 | 4 | 3 | 3 | 9 |
| | | | | | |
| 總計 | 5 | 4 | 4 | 7 | 20 + 13 = 33 |

依此可推導出原題目求解的式子:
- 甲先進門:5 x 4 = 20
- 甲乙不得同門:1 x 4 + 3 x 3 = 9 + 4 = 13
進出門問題
進出門問題是指在一個由房間和門組成的迷宮中,找出從一個特定房間移動到另一個特定房間的最快路徑。進出門問題在電腦科學中被廣泛研究,它是一個經典的組合最佳化問題。
問題陳述
給定一個由房間和門組成的迷宮,其中每個房間都有多個門連接到其他房間。從一個給定的起點房間移動到一個給定的終點房間,找出最短路徑。
解決方法
解決進出門問題,常用的方法有廣度優先搜尋(BFS)和深度優先搜尋(DFS)。
廣度優先搜尋(BFS)
BFS 從起點房間開始,逐步探索迷宮中所有與起點房間相鄰的房間。然後,探索與這些相鄰房間相鄰的房間,以此類推。這個過程重複進行,直到到達終點房間。BFS 保證找到最短路徑。
深度優先搜尋(DFS)
DFS 從起點房間開始,選擇一條路徑深入探索迷宮。如果遇到死路,則回溯到最近的選擇點,並選擇另一條路徑繼續探索。DFS 不保證找到最短路徑,但通常比 BFS 執行得更快。
演算法效率
下表比較了 BFS 和 DFS 的時間複雜度和空間複雜度:
| 演算法 | 時間複雜度 | 空間複雜度 |
|---|---|---|
| BFS | O(V + E) | O(V) |
| DFS | O(V + E) | O(V) |
其中,V 是房間的數量,E 是門的數量。
應用
進出門問題在許多實際應用中都有用,例如:
- 設計電子導航系統
- 路線規劃
- 網路連接最佳化
- 社交網路分析
範例
考慮一個由 5 個房間和 6 扇門組成的迷宮,如下圖所示:
| 房間 | 連接門 |
|---|---|
| A | B, C |
| B | A, C, D |
| C | A, B, E |
| D | B, E |
| E | C, D |
如果要從房間 A 移動到房間 E,BFS 將按照以下順序探索房間:A、B、C、D、E。因此,最短路徑為 A -> B -> C -> E,總共 3 扇門。
延伸閲讀…
深入探討直線排列行列式
甲,乙由不同門進出教室方法數 – YouTube
