六邊形及其特徵
正六邊形是一種具有六條邊和六個頂點的多邊形,同時具有邊可遞和點可遞性。它是一種雙心多邊形,具有內切圓和外接圓。此外,它是一種正多邊形,即其邊長和角相等。
六邊形的構造
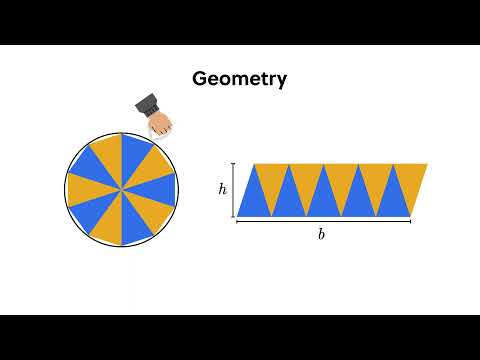

正六邊形可以用於尺規作圖。由於正六邊形由六個等邊三角形組成,其內切圓半徑為三角形的高,即邊長的三分之二根號三。
六邊形的特性

它的主要特徵包括:
- 內角和:720 度
- 每條邊長度:與外接圓半徑相等
- 邊心距:內切圓半徑,為邊長的三分之二根號三
- 內角:120 度
- 旋轉對稱性:階數為 6
- 軸對稱性:6 個對稱軸
- 最大對角線:邊長的兩倍,位於兩側頂點之間
六邊形的應用
正六邊形因其獨特的特性而廣泛應用於自然界和技術領域:
- 蜂巢:蜜蜂利用六邊形結構來最佳利用空間和建材。
- 玄武岩:在火山岩中形成六邊形柱狀結構。
- 苯分子:苯分子的結構呈六邊形環狀。
- 正二十面體:可以由 12 個正五邊形和 20 個正六邊形組成。
- 巴克明斯特富勒烯:一種由 60 個正六邊形組成的球形碳結構。
正六邊形的分類
根據其角的性質,可以將六邊形分為三種類型:
- 凸六邊形:所有內角小於 180 度。
- 凹六邊形:至少有一個內角大於 180 度。
- 星形六邊形:邊自我相交。
正六邊形的計算
以下是與正六邊形相關的一些計算公式:
| 公式 | 描述 |
|---|---|
| 內角和 | (n-2) × 180° |
| 其中 n 是邊數 | |
| 外接圓半徑 | t |
| 邊長 | t |
| 邊心距 | 2√3/3 t |
| 內切圓半徑 | √3/2 a |
正六角形角度:一個幾何奇觀的探索
正六角形以其六個等邊和六個相等的內角而聞名,在幾何學和日常生活中都扮演著重要的角色。本文將深入探討正六角形的角度,揭示它們獨特的性質和實用應用。
正六角形的內角
正六角形的內角和為 720 度。這是因為每個內角都是 120 度,這可以通過以下公式計算:
120 度 * 6 = 720 度
這種特殊的角度和可以追溯到正六邊形的對稱性。因為它有六條邊,所以可以沿著任意一個頂點旋轉 60 度,而仍然保持其相同的外觀。
表格:正六角形角度摘要
| 特徵 | 值 |
|---|---|
| 邊數 | 6 |
| 內角數 | 6 |
| 內角和 | 720 度 |
| каждой角 | 120 度 |
正六角形的外部角度
正六角形的外部角度為 360 度。這是因為每個外部角都是 60 度,這可以通過以下公式計算:
360 度 / 6 = 60 度
外部角度和等於 360 度是由於正六角形的平面的凸形性質。
正六角形的應用
正六角形角度在以下領域中具有廣泛的應用:
延伸閲讀…
六邊形
六邊形
- 建築結構: 六角形結構以其強度和穩定性而聞名,從蜂窩到屋頂架構都有應用。
- 化學: 苯環以其六角形結構而聞名,形成有機分子的骨架。
- 圖形設計: 正六角形形狀可用於創建標誌、徽章和其他視覺元素,利用其對稱性和視覺吸引力。
- 自然界: 雪花經常形成六角形,因為水分子中的氫鍵排列成這種獨特的結構。
結論
正六角形角度展現了幾何學的奇蹟。從它們精確的 120 度內角到它們實用的 60 度外部角,正六角形形狀在自然界和人類創造中都扮演著至關重要的角色。深入瞭解這些角度有助於我們欣賞正六角形形狀的獨特美感和實用性。
