方格填充的排列組合
這題歷年的學測排列組合題目中公認最難,甚至名師起初也採用窮舉的方式。然而,本文提供了更精巧的解析,一旦熟悉後便能輕易上手。
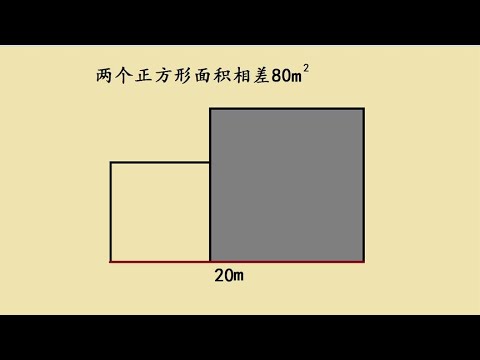

分析思路

方格填滿的關鍵在於凸出的部分,由於方塊必須填滿全部面積,因此排列受限。將凸出的部分視為矩形,再延伸至整個題目,即可化繁為簡。
| 步驟 | 分析 |
|---|---|
| 一 | 找出凸出部分的塞方格可能 |
| 二 | 將方格塞入後簡化題目 |
| 三 | 解決簡化的矩形題目 |
結論
此方法建立在對矩形排列組合的熟稔,透過將複雜題目拆解成簡潔部分,最終輕鬆解題。
12個正方形組成的房間地面:規劃與優化空間利用
一個房間的地面是由 12 個正方形所組成,每個正方形的邊長為 1 公尺。這些正方形可以排列成不同的形狀,以滿足不同的空間利用需求。
正方形排列的可能性
12 個正方形可以排列成以下幾種形狀:
| 形狀 | 佔地面積 | | 形狀 | 佔地面積 |
|—|—|—|
| 3 x 4 矩形 | 12 平方公尺 | | 4 x 3 矩形 | 12 平方公尺 |
| 2 x 6 矩形 | 12 平方公尺 | | 1 x 12 走道 | 12 平方公尺 |
| 1 x 4 x 3 L 型 | 12 平方公尺 | | 1 x 6 x 2 U 型 | 12 平方公尺 |
| 1 x 3 x 4 Z 型 | 12 平方公尺 | | 2 x 4 x 3 T 型 | 12 平方公尺 |
最佳排列選擇
選擇最佳的正方形排列取決於房間的形狀、大小和用途。以下是幾個考量因素:
- 房間形狀:矩形房間適合排列成矩形或走道形狀。正方形房間可以排列成任何形狀。
- 房間大小:較大的房間需要更大的正方形排列,例如 3 x 4 或 4 x 3 矩形。較小的房間則適合較小的排列,例如 2 x 6 或 1 x 12 走道。
- 用途:客廳、卧室或遊戲室等不同房間具有不同的用途,這些用途需要考慮在內。例如,客廳可能需要更大的開放空間,而卧室可能需要較小的私密空間。
規劃範例
假設有一個長 4 公尺寬 3 公尺的矩形房間。可以將 12 個正方形排列成以下形狀:
- 3 x 4 矩形:這是房間形狀最合適的排列。它提供了均衡的空間利用和移動空間。
- 2 x 6 矩形:這個排列可以營造較細長的空間,適合較長的傢俱或物品。
- 1 x 12 走道:這個排列提供了一個開放的走道空間,適合需要較大活動範圍的房間。
選擇最適合特定房間的排列時,應考慮這些因素和範例。透過仔細規劃,12 個正方形的房間地面可以充分利用空間並創造美觀且實用的環境。
延伸閲讀…
【學測】103 填充F 長方形磁磚鋪法| 評量專區 – 均一教育平台
大學入學考試中心103 學年度學科能力測驗試題數學考科
